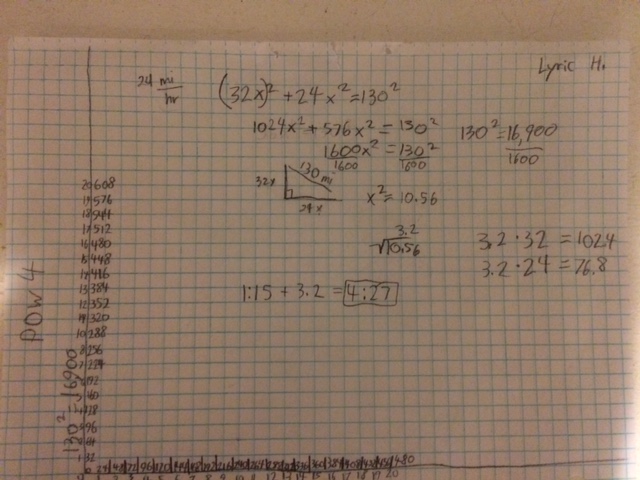Semester One Reflection
1. Describe one topic you feel you have mastered this semester. Describe the activities that helped you learn this activity. How do you know you have mastered this skill?
One topic I feel I have mastered this year, is Pythagorean theorem and triangles. This was fairly easy for me to comprehend, in all truthfulness. I had learned about lines and had done triangle work in years past, but this year, I feel like we really got somewhere with it. I know I’ve mastered the Pythagorean theorem because I use it whenever possible. On a worksheet, if there is a picture of a triangle and it asks what the length is of the hypotenuse, I always use the pythagorean theorem even if it’s not a right triangle. I always start there, because I know it, and it never hurts to try. I even enjoy doing it because I know it. I have chosen three pieces of evidence. They are POW 3, POW 4, and my Triangles Quiz, all of which used the Pythagorean theorem.
One topic I feel I have mastered this year, is Pythagorean theorem and triangles. This was fairly easy for me to comprehend, in all truthfulness. I had learned about lines and had done triangle work in years past, but this year, I feel like we really got somewhere with it. I know I’ve mastered the Pythagorean theorem because I use it whenever possible. On a worksheet, if there is a picture of a triangle and it asks what the length is of the hypotenuse, I always use the pythagorean theorem even if it’s not a right triangle. I always start there, because I know it, and it never hurts to try. I even enjoy doing it because I know it. I have chosen three pieces of evidence. They are POW 3, POW 4, and my Triangles Quiz, all of which used the Pythagorean theorem.
|
ANNOTATIONS FOR POW 3
As you can see, I used the Pythagorean theorem multiple times throughout the problem. I got 10/10 on this problem. |
ANNOTATIONS FOR POW 4
In this POW, I did more than just the Pythagorean Theorem. It was a complicated one, using the theorem and multiplication and time and all that good stuff, but the core majority of it was Pythagorean. I got 9/10 on this part, but it wasn't the math I got wrong, it was part of the write-up. |
ANNOTATIONS FOR TRIANGLE QUIZ
This quiz was based around triangles and the Pythagorean Theorem. I used it many times throughout, and these are some of the clearest examples. I aced this quiz.
This quiz was based around triangles and the Pythagorean Theorem. I used it many times throughout, and these are some of the clearest examples. I aced this quiz.
2. How have the Explorations (and group discussions of Explorations) changed your experience as a math student this year? In what ways have they made math class more challenging, and in what ways have the Explorations and discussions helped you learn?
I hadn’t had real math homework in a long while, or at least, something for me to get a little stressed and mad about, so it was nice to have explorations. I don’t think that the discussions about them were that helpful, mainly because when we had discussions, it just turned into the teacher giving us the answers and no discussing. Explorations have definitely made this year's math class feel more like a real math class. I feel like we’re actually completing something. I love project based learning, but having a little bit of traditional school stuff like that is refreshing.
3. What is the hardest math problem you have encountered this semester? Explain how you solved it, or if you didn’t, why you weren’t able to.
One of the hardest math problems I had to solve this year was POW 7. It had nothing really to do with math, but it had to do with critical thinking. I’m not sure I even get it still, but we did find the right answer. By we, I mean Colin and I. He solved it by thinking it through in his head. I tried countless times to understand the method he had taken. It made sense at first, but then it got spotty, with a lot of guess and check going on. I relied on Colin for the most part and i should’ve tried more, but it was too hard to comprehend.
I hadn’t had real math homework in a long while, or at least, something for me to get a little stressed and mad about, so it was nice to have explorations. I don’t think that the discussions about them were that helpful, mainly because when we had discussions, it just turned into the teacher giving us the answers and no discussing. Explorations have definitely made this year's math class feel more like a real math class. I feel like we’re actually completing something. I love project based learning, but having a little bit of traditional school stuff like that is refreshing.
3. What is the hardest math problem you have encountered this semester? Explain how you solved it, or if you didn’t, why you weren’t able to.
One of the hardest math problems I had to solve this year was POW 7. It had nothing really to do with math, but it had to do with critical thinking. I’m not sure I even get it still, but we did find the right answer. By we, I mean Colin and I. He solved it by thinking it through in his head. I tried countless times to understand the method he had taken. It made sense at first, but then it got spotty, with a lot of guess and check going on. I relied on Colin for the most part and i should’ve tried more, but it was too hard to comprehend.
Habits of a Mathematician
- Generating ideas
- Communicating thinking in a clear and accessible way
- Recognizing and resolving errors
- Reflecting and synthesizing
1. Which Habit of a Mathematician do you feel you have the most mastery over? Explain what this skill is and what it means to you. Explain how you have demonstrated this skill, the activities that helped you develop this skill, and how you have grown in that problem-solving skill this semester.
The habit of a mathematician that I feel I have the most mastery over is generating ideas. To me, this means that i come up with ideas of how to solve the problem right when we get the problem. Let's say that a new POW was just released and I was reading it for the first time. I would automatically start to solve it in my head and start to generate how to write how I got my answer in words for the writeup later on. I have demonstrated this skill on every POW we have done this year. I did POWs last year, so doing them again this year helped improve my writing and explaining and problem solving.
For example, here are the intros and explanations for POWs 3 and 4.
The habit of a mathematician that I feel I have the most mastery over is generating ideas. To me, this means that i come up with ideas of how to solve the problem right when we get the problem. Let's say that a new POW was just released and I was reading it for the first time. I would automatically start to solve it in my head and start to generate how to write how I got my answer in words for the writeup later on. I have demonstrated this skill on every POW we have done this year. I did POWs last year, so doing them again this year helped improve my writing and explaining and problem solving.
For example, here are the intros and explanations for POWs 3 and 4.
|
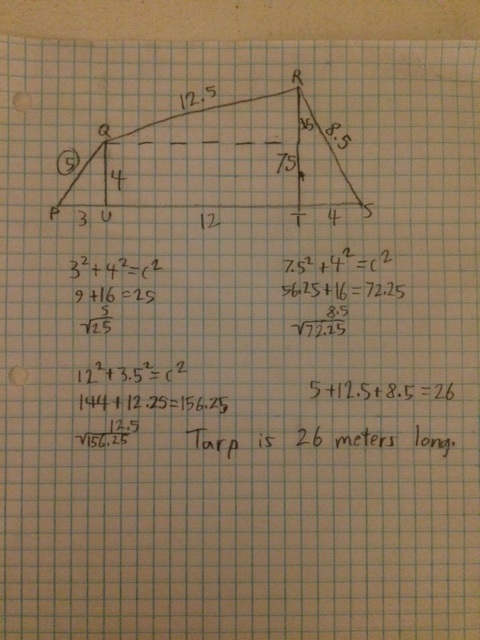
POW 3
This problem of the week is about some random people setting up a tent. They put up two poles, one is 4 meters tall and the other is 7.5 meters tall. The set a tarp on top of those two poles and secure them on either side. On the side of the 4 meter pole, they secured it 3 meters away. On the side of the 7.5 meter pole, they secured it 4 meters away. You need to find the length of the tarp. A rough prediction on what I thought the answer would be, is around 25-30 meters for the tarp. Somewhere in that range. When I started this problem, I knew instantly that it was the Pythagorean Theorem. I got to work on the 4 meter tall pole with the tarp coming out 3 meters. I knew that 3,4,5 was a Pythagorean triple, so that side was easy to answer. I then switched to the other side, the 7.5 meter tall pole with the tarp coming out 4 meters. I used the Pythagorean Theorem for this side and got 8.5. Now that I had the two lengths of the outside, I needed to get the third one. Since one pole was 7.5 meters tall, and the other was 4 meters tall, I realized a triangle could be made since there was a 3.5 meter height difference between the two poles. I used that height, and the base, which was 12 meters (original base of the poles), and used the Pythagorean Theorem again. I got a length of 12.5 for the part of the tarp. I then added 5+12.5+8.5 and got 26 meters. |
ANNOTATIONS FOR BOTH
I start off by rewriting the problem in my own words, then explaining how I got my answer. The explanation is always being thought up before hand. Once I have the general idea, I get out a piece of paper and answer the problem. |
POW 4
Our fourth Problem of the Week was a glorified pythagorean theorem problem. The two people left the store at 1:15. One person, Maya, is traveling north at 32 miles per hour. The other person, Jason, is traveling east at 24 miles per hour. We need to find out how many hours, or how long it’ll take for them to be 130 miles apart and how far each person traveled to get there. I actually had no prediction for the answer to this POW. I looked at it and just blanked. Once I started writing out everything I knew, I just started to solve it. Todd actually helped me get started answering the POW. I started by finding 130 squared. I knew it had to do with the Pythagorean theorem. Once I had that answer, I changed direction and started from what the other side. I took 32x and 24x and made the equation (32x) squared + (24x) squared = 130 squared. I then found 32x squared and that equaled 1024x squared. 24x squared equaled 576x squared. Once again, the equation equaled 130 squared because the equation wouldn’t add up yet. 1025+576=1600. It was now 1600x squared equals 130 squared. I then used the square of 130, which was 16,900. I then dived 1600 and 16,900 by 1600. I was left with x squared equals 10.56. I then found the square root of 10.56. It equaled 3.2. Once I had found the amount of time it took, 3.2 hours, I added it to 1:15. .2 of an hour is 12 minutes, just so you know. It ended up being 4:27 when they got to there homes. Now I had to find how many miles they rode. I took 3.2 and multiplied it by 32 mph. Maya rode 102.4 miles home. Again, I took 3.2 and multiplied it by 24 mph. Jason rode 76.8 miles home. |
2. For which Habit(s) do you feel you have the most room to stretch? What do you think held you back from improving in this skill this semester?
The habit or habits of a mathematician that I feel I have the most room to stretch in, is reflecting and synthesizing. All reflection seem a little hard to me. I go into them thinking that it’ll be easy, but I never know how to say what I want to. We’ve had quite a lot of time to actually reflect on things, but there is just something that keeps holding me back. It could be that I just don’t understand the question completely or I am over thinking the question.
The habit or habits of a mathematician that I feel I have the most room to stretch in, is reflecting and synthesizing. All reflection seem a little hard to me. I go into them thinking that it’ll be easy, but I never know how to say what I want to. We’ve had quite a lot of time to actually reflect on things, but there is just something that keeps holding me back. It could be that I just don’t understand the question completely or I am over thinking the question.